200以上 三角形角度 180 288673

数学科目 将五角星看作是5个重叠在一起的三角形 即五个三角形的和为5乘以180°为900° 再减去五角星中间的那个五角形的 それは三角形の角度の合計に関する定理から直接見つけられる：α＋β＋γ＝ 180°＝＞γ＝ 180° α β＝ 180° 30° 63°＝ 87°。 2 今度はより一般的な形の三角形の3番目の角度を見つける問題を考えてみましょう。 师：利用直角三角形来证明了锐角三角形和钝角三角形的内角和，其实我们还能利用一支铅笔来证明，你们听说过吗？ 师：观察这两支笔，现在你有什么发现？ 预设生：铅笔的方向发生了改变，铅笔旋转了一个平角,平角是 180°，说明三角形的内角和是 180°。

三角函数和向量 Swazer Z 程序员资料 向量与三角函数 程序员资料

三角形角度 180

三角形角度 180- 直角三角形，两夹角相加等于90° float α = 90 β; 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 三角形の内角の和というのは，三角形の内側の角の大きさの和のことをいいます。 三角形の内角の和＝180° 小学生女の子 正三角形の1つの角の大きさが60°で角は3つだから

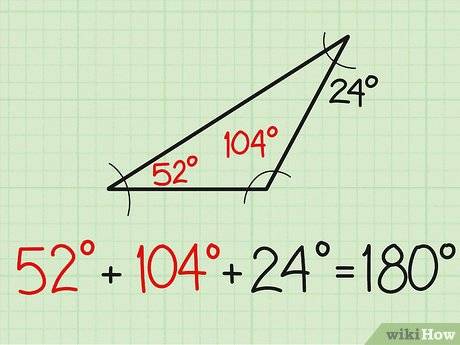
如何求三角形的第三个角 大小

 ） 但是球面三角形的情况，如果q只在一个平面上转，虽然角度总和是180度，但是这样的三角形只有一种，就是其中两点取在南极北极，构成一个0 0 180度的三角形。 而只要q不是在一个平面上转，那么它转过的角度就不止180度，因此球面三角形的内角和大于180度。 今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ＝となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質 "三角形的内角和是 180 度"，这一结论在人教版义务教育课程标准实验教科书四年级下册第五单元第 6 小节三角形的知识学习中，学生通过动手操作已经得出，而本学期学生已经学习了平行线的性质与判定、平角的知识，学习了平移的知识，初步感受了几何推理的结构，本节课是在此基础上

角度和弧度的公式关系： 角度 = 弧度 / π * 180 弧度 = 角度 / 180 * π 3、直角三角形，已知一直角边a，和夹角∠α，求边长b //边长b = 夹角∠α乘以邻边a float b = α * a; これは、三角形ABEと三角形CDEで見た時に、対頂角eがそれぞれ等しいため、三角形の内角180°から対頂角eを引いた角度がそれぞれ等しいからです。 180－∠e＝∠a＋∠b（三角形ABE） 180－∠e＝∠c＋∠d（三角形CDE） よって、 ∠a＋∠b＝∠c＋∠d等腰直角三角形(Isosceles triangle)是一种特殊的三角形，具有所有三角形的性质：稳定性，两直角边相等 直角边夹一直角锐角45°，斜边上中线角平分线垂线 三线合一，等腰直角三角形斜边上的高为外接圆的半径R，那么设内切圆的半径r为1，则外接圆的半径R就为√21，所以rR=1(√21)。

 等边三角形是等腰三角形的一个特殊形式。 等腰直角三角形只有一种形状，其中两个角为45度。 10退化三角形 退化三角形的面积为零。这种三角形通常只有几类：如果一个三角形内的三只角的角度分别为(180,0,0)或 (90,90,0)，则它是一个退化三角形。三角函数（英語： Trigonometric functions ）是數學中常見的一類關於角度的函数。 三角函數將直角三角形的内角和它的两個邊的比值相关联，也可以等价地用与单位圆有关的各种线段的长度来定义。 三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究振动、波、天体运动以及各种周期三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。

三角形角度计算中的整体思想 参考网

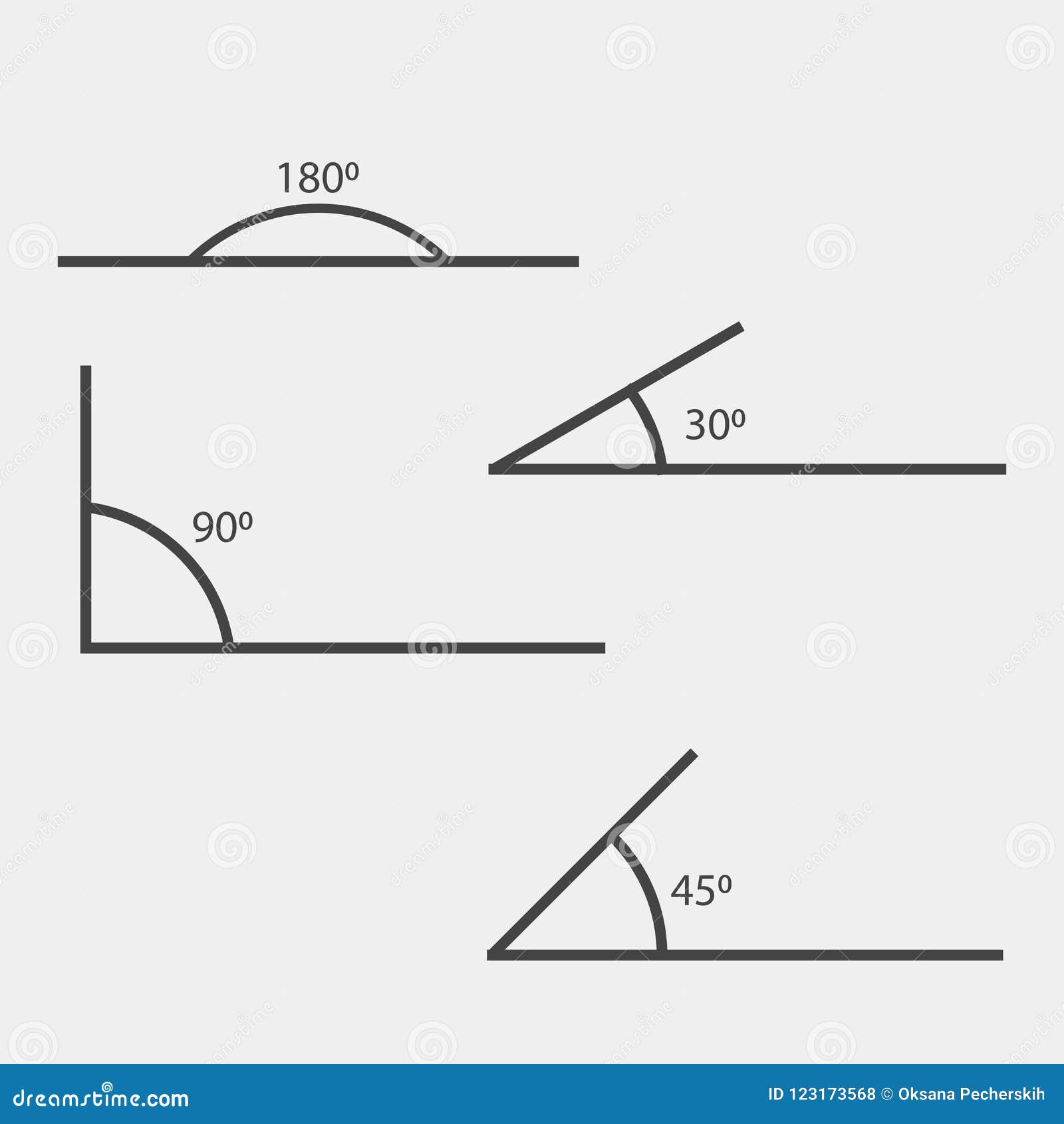
角度180 45 30 90度导航例证标志o 向量例证 插画包括有完全 图标 长期 要素

三角形中的角度计算 已知等腰三角形的一个底角为 2 n°，则另一个底角也是 n°,顶角为 180°－2n° 三角形中的角度计算主要分以下三种形式： 1、方程法，2、推理代换法，3、特殊值法 1、方程法 例 1、在 abc 中，ab=ac，cd 平分∠c，∠adc=150°，求∠b 如果您仍然热衷于了解有关直角三角形的更多信息，请查看这些三角函数。 正弦 sin α = 对边 / 斜边 余弦 cos α = 相邻/斜边 切线 tan α = 对面/相邻 了解了这些，您可以轻松计算直角三角形的边，甚至可以使用下面的三角函数表确定角度。 这方面的一个回答 (3件中の1件目) 曲がった空間での三角形は180度を超えることがあります。近くに地球儀があれば確認してみてください。第1点を北極点にとります。子午線に沿ってまっすぐ90度移動します。赤道に到達したはずです。進路を90度だけ変えて赤道上を, 経度にして90度移動します。そこで進路を

等腰三角形求度数的公式一些有关于求三角形度数的公式 完整点 朵拉利品网

三角形 09 任意三角形三內角和等於180度的證明1 Youtube

星形の内角の和が180°になる理由 星形の角度が180°になる理由を説明していくために 三角形の外角の性質を知っておく必要があります。 このように 三角形の外角は、隣にない内角2つ分を合わせた大きさになるという性質があります。 これを利用して 已知三角形边长，计算三角形的角度过程如下： 1、设三角形中角A所对应的边长是a，角B所对应的边长是b，角C所对应的边长是c。 再利用公式： ①CosA= (c^2b^2a^2)/2bc ②CosB= (a^2c^2b^2)/2ac ③CosC= (a^2b^2c^2)/2ab 算出每一个角的余弦值，利用计算器上的反余弦函数 Js求角度、三角形 // 你可以用这个公式知道任何直角边的角度： Mathasin(sinOfAngleX) * 180/MathPI 使用sinOfAngleX = 05,Mathasin(sinOfAngleX)将给出这用弧度表示要将其传递到度数,您可以乘以180 / MathPI,结果为30

1

三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun

 三角形の内角 三角形の3つの内角の和 → 必ず180°になる 問題 xの角度は？？簡単だね？3つの内角を全て足し算すると180°だから、 40°65°∠x＝180° ∠x＝75°・・・（答え） 三角形の 18 180 21无论是锐角三角形，直角三 角形还是钝角三角形，它们 的内角和都是180。 22三角形越大，它的内角和就越大。 一个三角形的三个内角度数是：70,64,45。 （三）应用新知，解决问题23 在一个三角形，1=140， 3=25，求2的度数 24 求出三角形各个角的度数。解説＆答えはこちら 答え 二等辺三角形が2つくっついている問題ですね。 この場合、それぞれの二等辺三角形に注目して角度を1つずつ求めていきます。 赤い二等辺三角形は、頂角が36°なので 底角1つ分の角は となります。 そこから、次は青い二等辺

1

數學措施 數學樂趣 數學珍寶 力拓學區

杏山中心校教学设计 年级 四年级 任课教师 周显杰 教学内容 探索与发现（一）（探索和发现三角形内角和等于180°） 教学目标 1．通过操作活动探索发现和验证"三角形的内角和是180度"的规律。2．在操作活动中，培养学生的合作能力、动手实践能力，发展学生的空间观念。 こんにちは、ウチダです。 今日は、中学2年生で詳しく学ぶ 「三角形の内角の和」 について、それが180度である証明や、三角形の外角に関する公式・問題を解説していきます。 また、記事の後半では「内角の和が270度である三角形」についても考察し

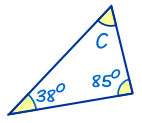
三角形里有180度

这题没有思路 你不妨换个角度看看 三角形 直角 斜边 正方形 线段 手机网易网

初中数学角度计算的经典模型 会了这几种求角度的题目就很简单了 壹读

准备好学习直角三角形和三角学 文章 直角三角形的比例 可汗学院

等腰三角形边长公式表等腰三角形边长公式计算器 简笔画图片库

180度的角怎么画图片 万图壁纸网

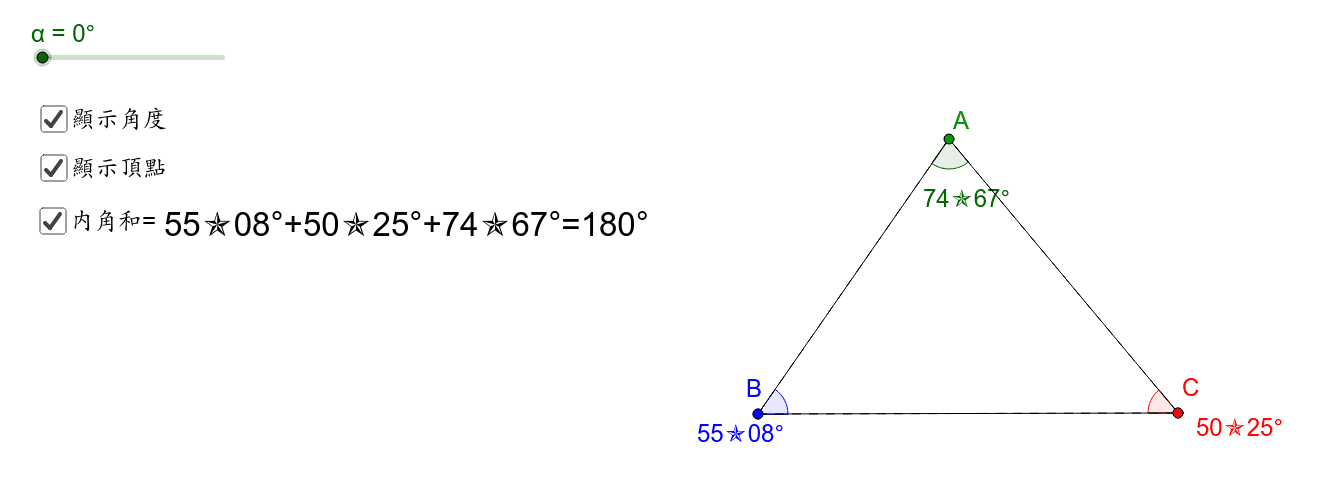
三角形內角和為180度 Geogebra

三角形内角和为180度 这个问题数学家研究了两千多年

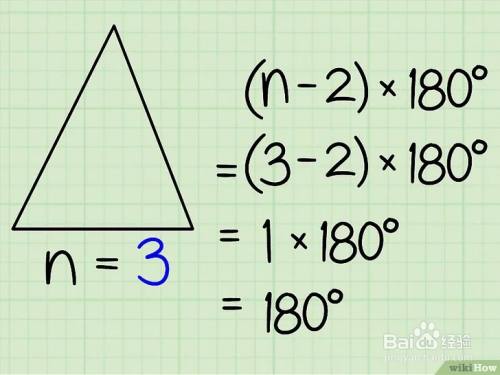
如何计算角度 百度经验

关于角度问题的奥数题 小初高题库试卷课件教案网

腾讯视频

Hdhf2q22fzczim

1

小５ 算数 小５ ３１ 三角形の角 Youtube

1

最も選択された 三角形角度定理 ニスヌーピー壁紙

三角形の内角の和は180度って証明できるの 三角形の外角の定理 公式 や問題アリ 遊ぶ数学

我們都生活在空間中 但到底什麼纔是空間 它有形狀嗎 雪花新闻

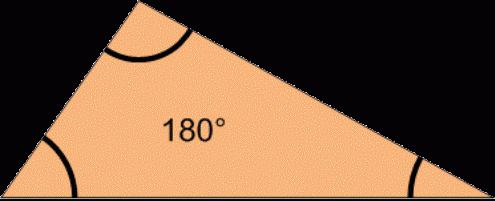
三角形的角度的总和 上的三角形的角度之和的定理

70以上三角形3 4 5 角度 シモネタ

角度计算公式图解 搜狗图片搜索

三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun

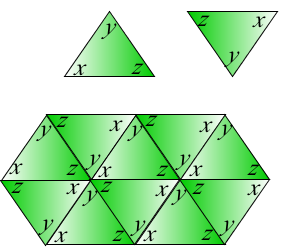
多边形的角和 数学和多媒体 必威app下载

怎么求三角形的第三个角 生活百科

三角形 维基百科 自由的百科全书

三角形の角度を求める問題がわかりません 三角形の和と直線の角度 Yahoo 知恵袋

锐角三角形的度数 说三角形内角和为180度是不对的 尚书坊

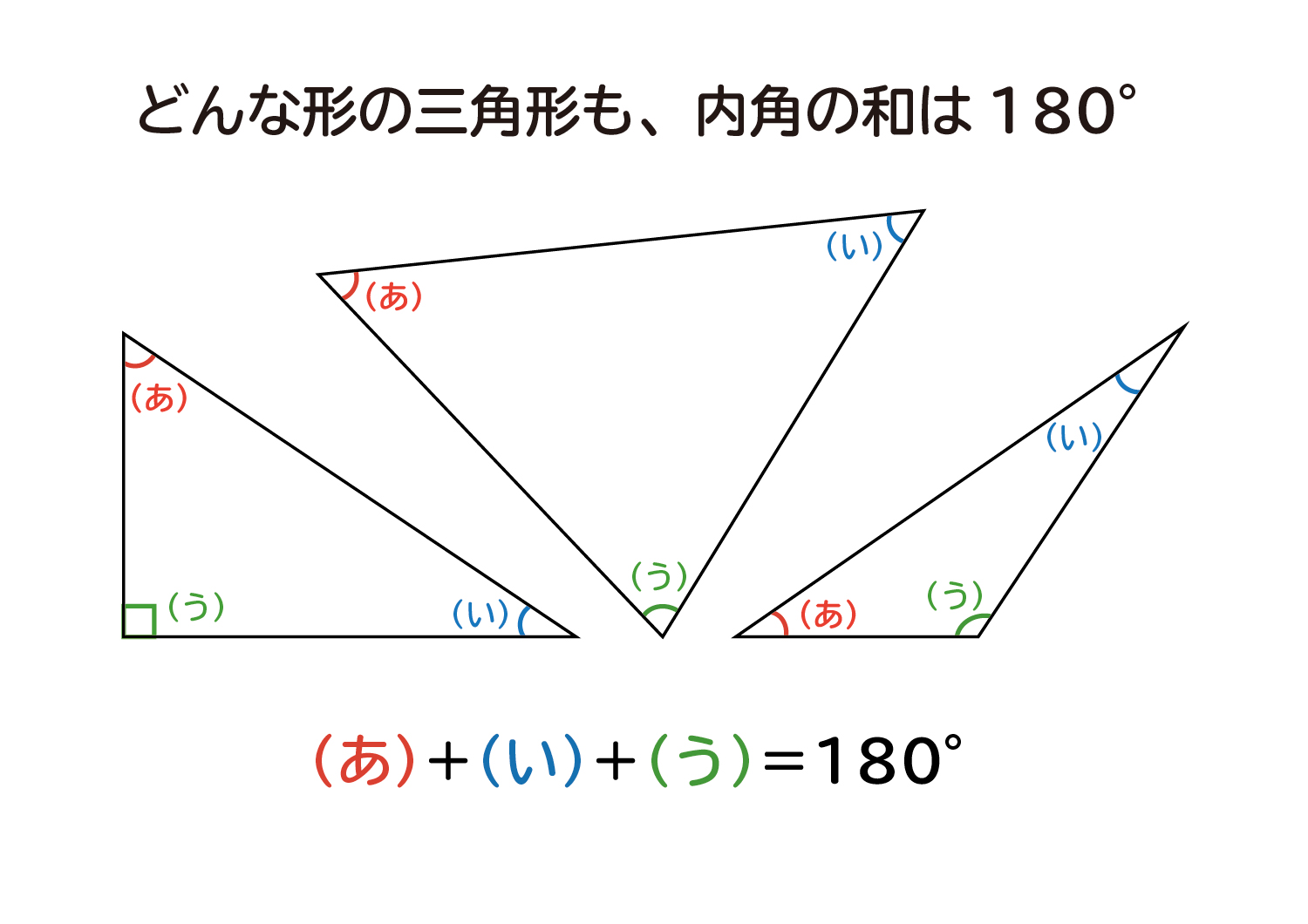
なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル

三角形 13 等腰三角形內角計算的基本題型 Youtube

求三角形内角度数图片 第1页 要无忧健康图库

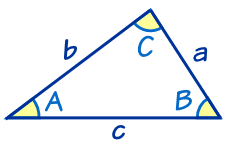
解三角形

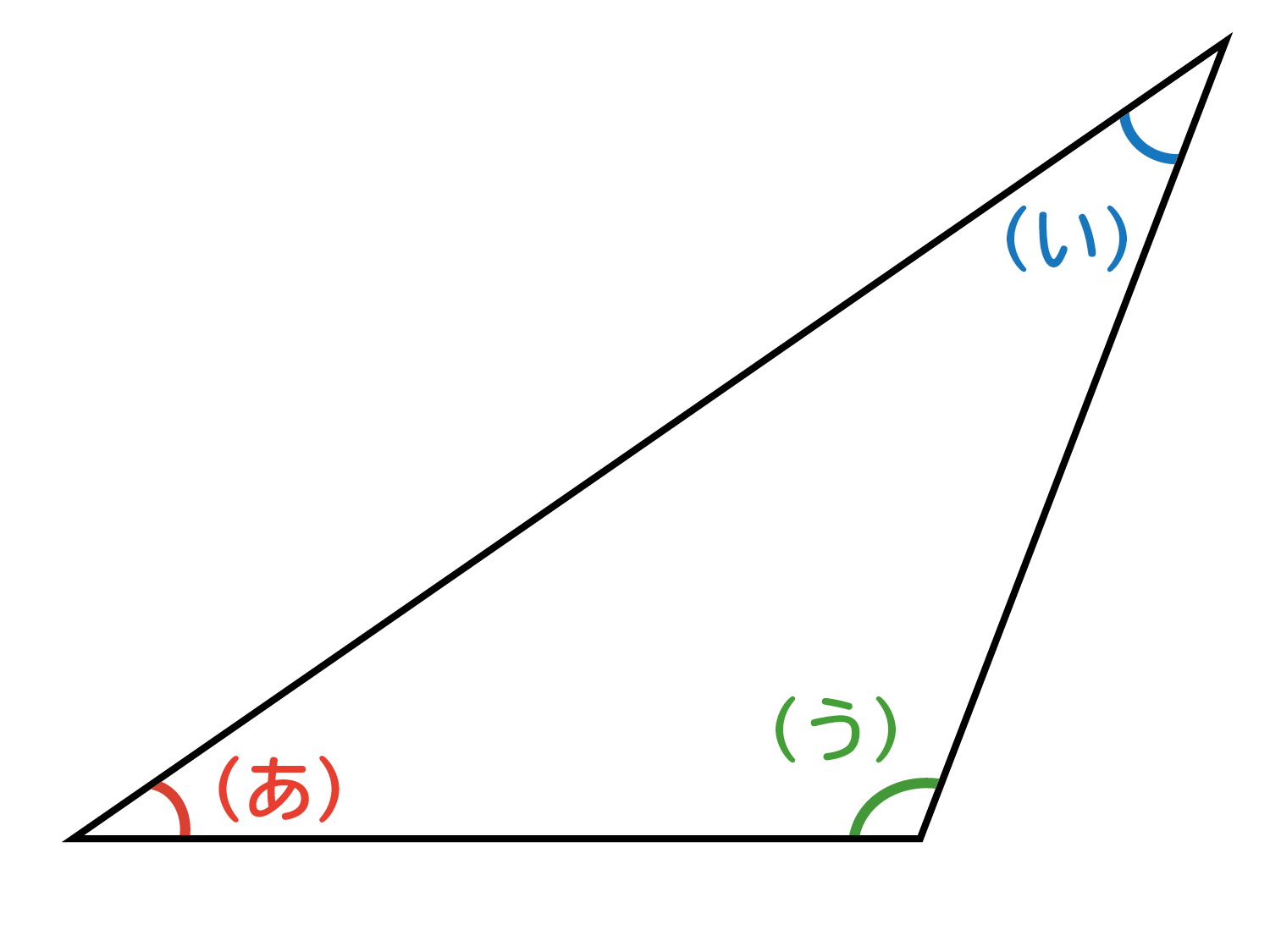
なぜ 三角形の 内角の和は180 なのか を説明します おかわりドリル

三角函数和向量 Swazer Z 程序员资料 向量与三角函数 程序员资料

如何计算角度 8 步骤 包含图片

证明三角形的角度之和的性质 提示 21

怎么求三角形的第三个角 生活百科

如何计算角度 8 步骤 包含图片

怎么求三角形的第三个角 生活百科

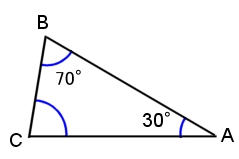
三角形の作る角度１ ３

初一数学 专题突破 三角形的计算与证明

直角三角形の解法 1

知道三角形一个角的度数 怎么求出另外两个角度数 比如一个三角形 我知道它一个角的度数 怎么求其它两个角的度数 知道三角形的内角和是180 如果答的清楚有明白的 作业帮

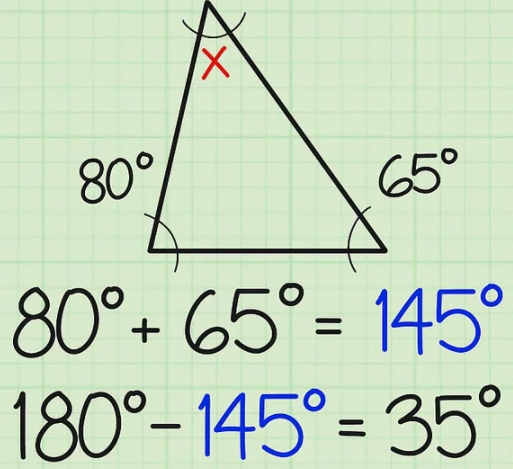
三角形的角度怎么算 两个方法帮你搞定 小学学习方法 小学升分技巧 向光学习平台

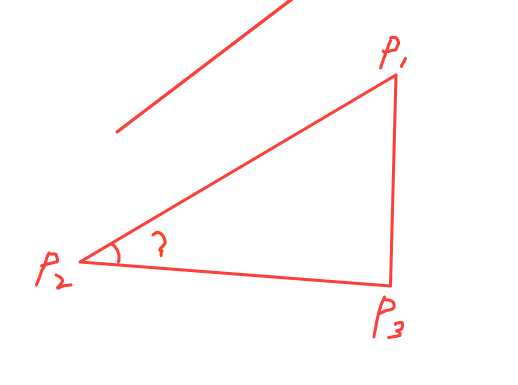
Swift 计算三角形角度 两条边夹角 那一抹风情 博客园

三角形内角和180度图解 第1页 要无忧健康图库

如何在梯形中找到角度 数学21

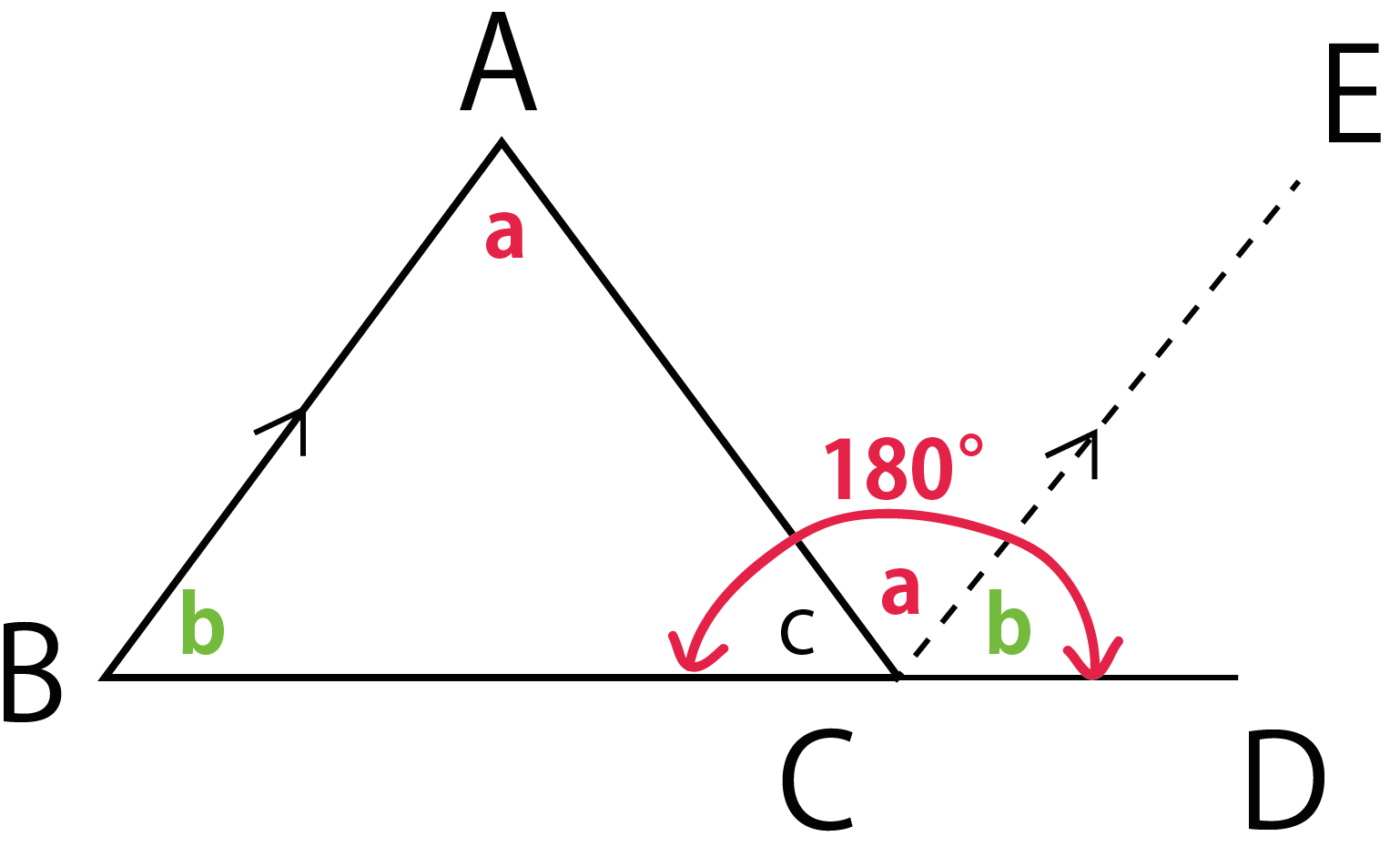
中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

数学都搞不好 你还搞什么游戏开发 知乎

中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

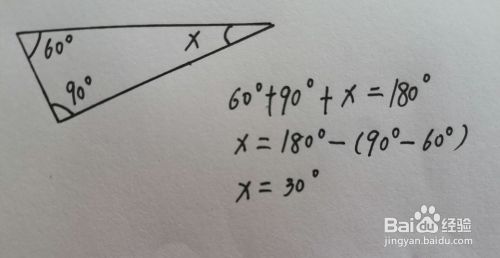
怎么计算数学中的角度呢 百度经验

四下 每日一题 角度计算01 哔哩哔哩 つロ干杯 Bilibili

搜索标签 将角度度量识别为加法第1页 满妈家庭课 您和孩子的一种亲近方式

等腰三角形公式角度等腰三角形的性質 高三網 Prlvr

角度180 45 30 90度导航例证几何 数学的标志设置包括角度的传染媒介象向量例证 插画包括有

三角形角度计算公式利用计算器上的反余弦函数功

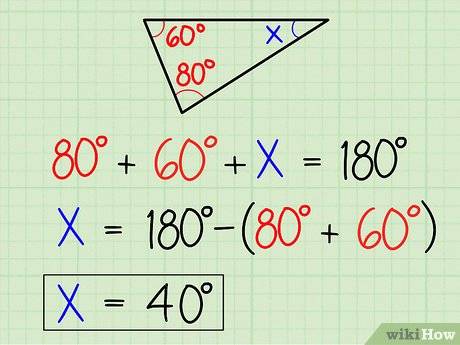
如何计算角度 度数

一个 8字模型 搞定五角星五个顶角度数之和 旅游资讯 娱乐新闻网

三角形 维基百科 自由的百科全书

如何求三角形的第三个角 社会 October 21

三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun

Opencv Python学习笔记 十三 霍夫变换 Mmagicloren的博客 程序员信息网 Opencv Python 霍夫变换 程序员信息网

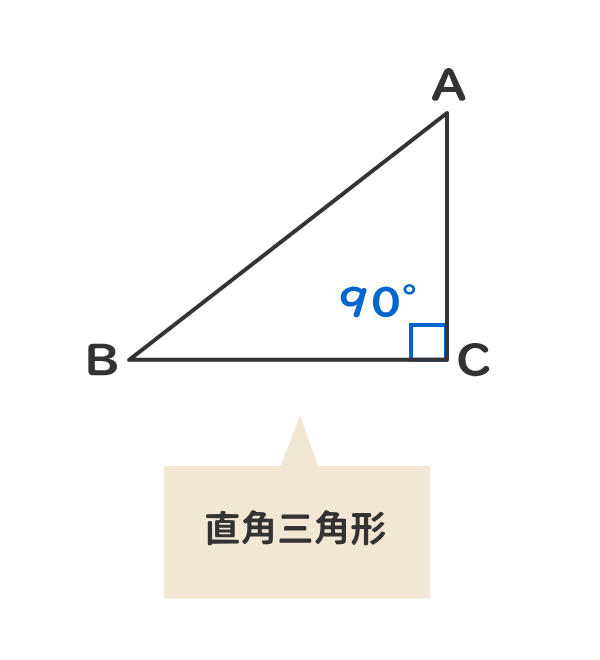
二つの特別な直角三角形の角度と辺の長さの比の関係を暗記しよう 電験3種web

使用opencv在python中进行线检测 码农家园

腾讯视频

如何找到内角 数学21

初中数学培优八年级上第一讲三角形的概念和性质 每日头条

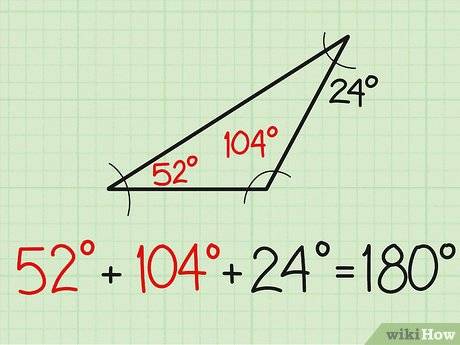
如何求三角形的第三个角 大小

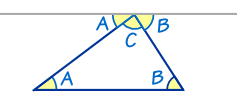
三角形里有180度

三角形内角和 简书

四年级角度图形题 求小学四年级几何三角形求角度数的题目 附加图 在线等 三人行教育网 Www 3rxing Org

树立方程思想求角度 第十五章复习 初中冀教版 数学中国网

如何求三角形的第三个角 社会 October 21

菱形的面积是多少 教育小本子

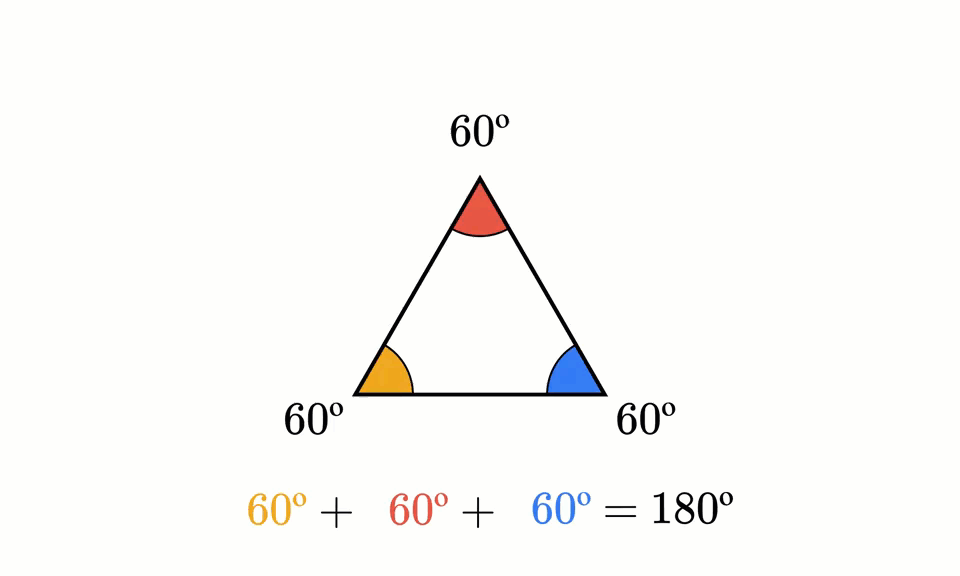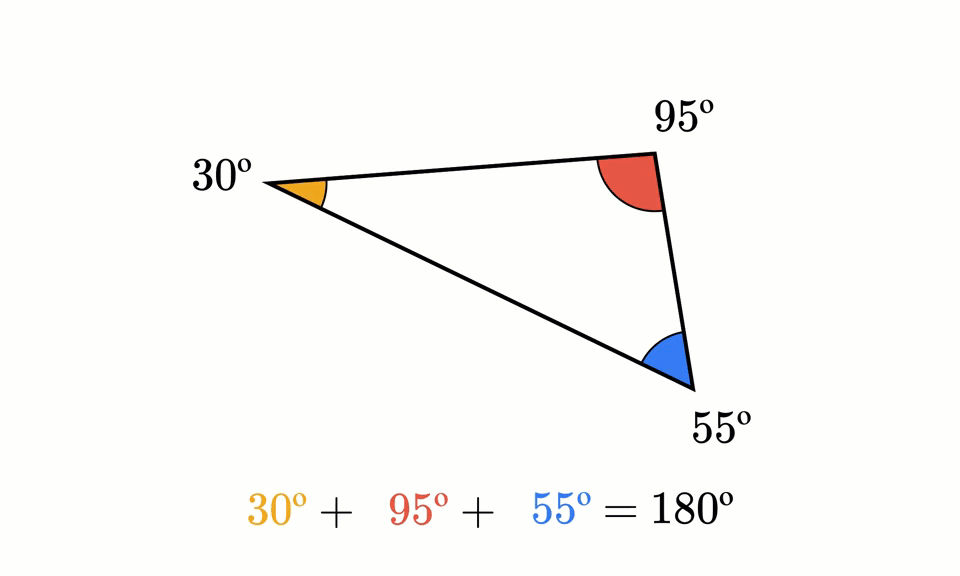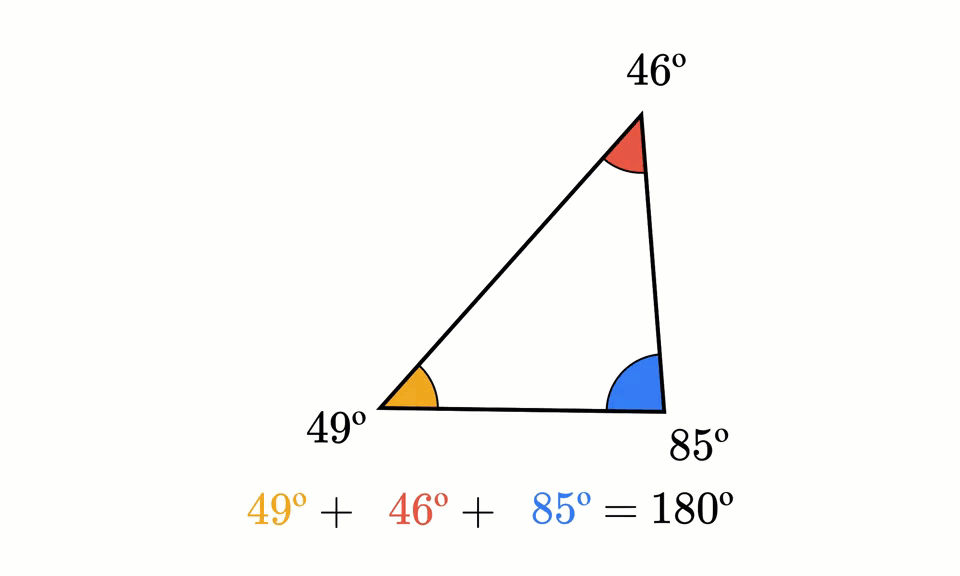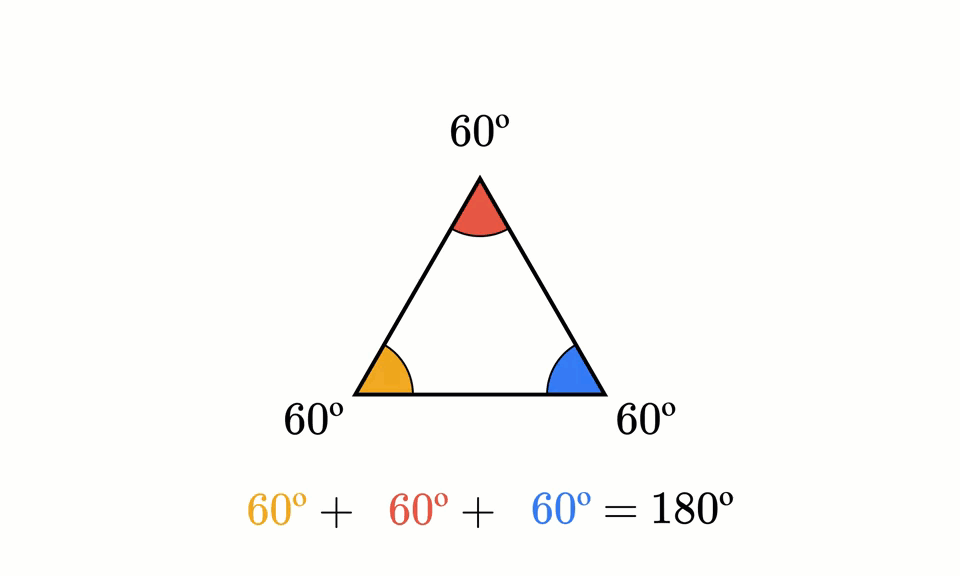
趣题分享 角度问题系列 哔哩哔哩

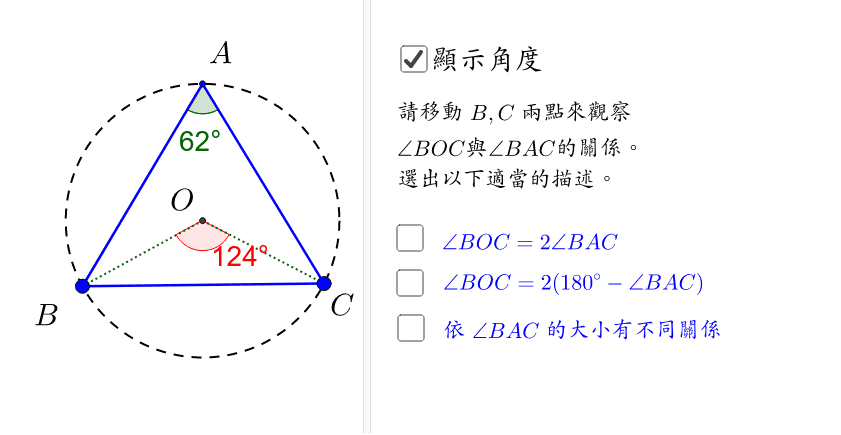
三角形外心的角度關係 Geogebra

三角形の内角の和が180度である理由と外角の和や多角形の公式 まぜこぜ情報局

Excel中的sin 公式 示例 如何在excel中使用正弦函数

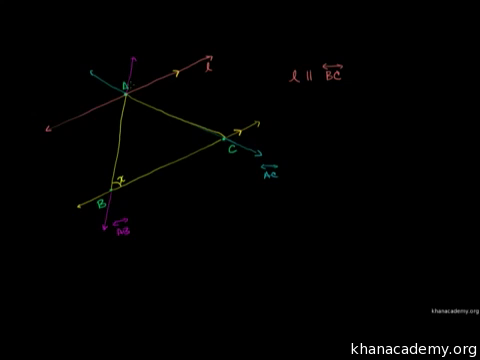
三角形内角和是180 的证明 视频 三角形的角 可汗学院

三角形内角和 简书

计算三角形角度 西瓜视频搜索

如何证明三角形是矩形 数学21

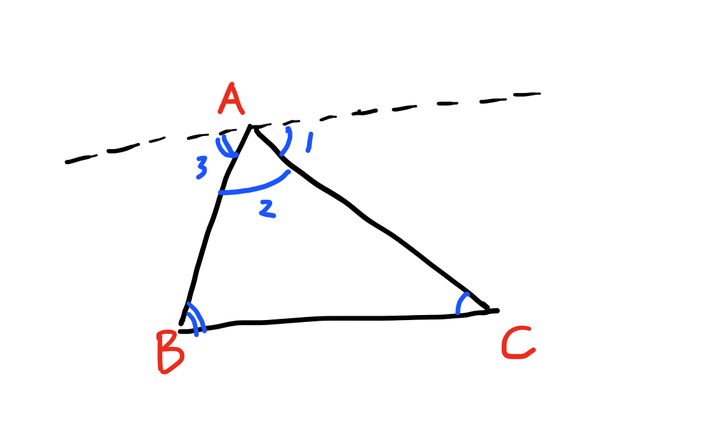
为什么三角形内角和一定是180 度 知乎

如何求三角形的第三个角 社会 October 21

多边形的角和 数学和多媒体 必威app下载

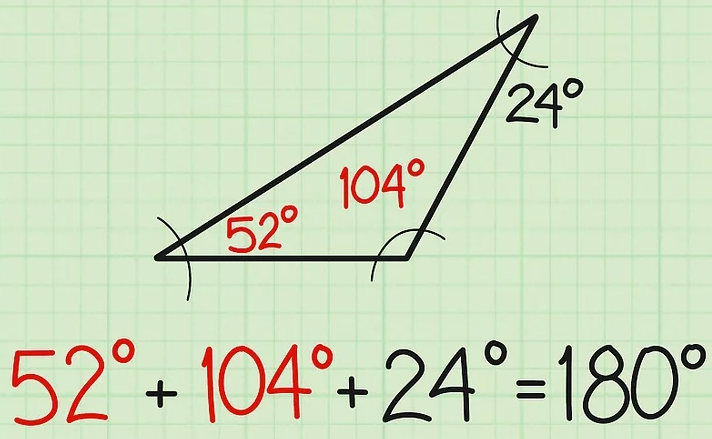
三角形的角度怎么算 两个方法帮你搞定 小学学习方法 小学升分技巧 向光学习平台

八字形三角形 万图壁纸网

三角形内角和定理 平行线的证明ppt 第1课时 第一ppt

三角形角度计算方法 西瓜视频

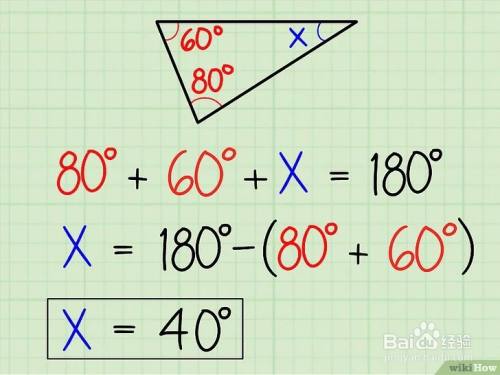
如何计算角度 百度经验

初中数学角度计算的经典模型 会了这几种求角度的题目就很简单了 壹读

三角形角度计算中的整体思想 参考网

八年级数学提优 老师解析 全等三角形的性质在角度计算中的运用 网易订阅

如图 在三角形abc中 角acb等于90度 角abc等于30度 将三角形abc饶点c按顺时针方向旋转角度a得三角

知道内角度数怎么求边数 扒拉扒拉

3种方法来求三角形的第三个角

三角形有关的角度计算 360文档中心