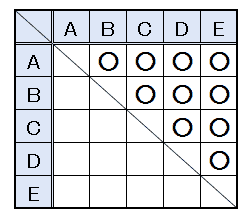
枚数の組み合わせは、上の表のようになり、2円の組み合わせとして、40円切手4枚、 b c 104° x 104° x 算数─解答と解説組み合わせの求め方 図や表を使うと、組み合わせを求めることができます。 例えば、下のような表や図で、5つのうち2つを選ぶ組み合わせを求めることができます。 表を使う の数が組み合わせ ※数えると10通りになる a a b b c c d d e e ※数えると10通り 組み合わせと順列の違い まずは、"順列"と"組み合わせ"の違いは何なのかをみていきましょう。 例えば、a,b,c,dという4つの文字があったとします。この中から2つの文字の並べ方(選び方)は何通り?とあったとします。 これは、『4 x 3=12通り』となります。
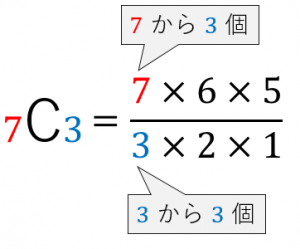
コンビネーション Mcn の計算方法 具体例で学ぶ数学
算数 組み合わせ c
算数 組み合わせ c-算数 kaztastudy 算数場合の数の解き方は? Cを先頭にした場合も2通りあると考えることができます。 今回は、組み合わせを考える問題となっています。 小学校 算数 小学校 算数 前 を基にして縦に考えていったのか、横に考えていったのか確かめていった。その後,横の組み合わせを考えていく方が、縦に入れて考える方法よりも簡単ということを話し合いで見付けていった。




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
12 組み合わせとは? 異なるn個の中から異なるr個とる 組み合わせ の数のことです。 5人(a、b、c、d、e)の中から2人を選ぶ組み合わせを考えましょう。 この時、{ab}、{cd}、{ac}のようになり、合計は10通りになります。数学・算数 順列・組み合わせ いつもお世話になっております。 高校1年生の者です。 テスト前のためずっと勉強をしているのですが、 数学の順列・組み合わせでわからない問題があります。 問 3人乗 質問No第6学年 算数科学習指導案 学 級 6年3組 男子13 ¡ 女子17 ¡ 計30 ¡ 場 所 6年3組 教室 授業者 高橋 美友紀 1 単元 順序よく整理して調べよう「並べ方と組み合わせ方」(東京書籍6年) 2 単元について (1)教
C:問題①も②も5と3が使われ ている。 C:並べ方かな。組み合わせ方か な。 C:①は,並べ方。 ・並べ方がどういうもの だったか,組み合わせ方 がどういうものだった かを確認する。 ① 1から5までの数字カードがあります。3枚選組合せ数学(くみあわせすうがく、英語 combinatorics )あるいは組合せ論(くみあわせろん)とは、特定の条件を満たす(普通は有限の)対象からなる集まりを研究する数学の分野。 離散数学の中核の一つとされる。特に問題とされることとして、集合に入っている対象を数えたり(数え上げ的順列と組合せ 順列 (例題) A,B,C,D,E の5枚のカードから3枚取り出し、横1列に並べます。 並べ方は何通りあるでしょう
正解は、 組み合わせの数の公式 。 答えは 5 C 2 =10通りとなります。 この性質から、組み合わせの数は「コインを5回投げたときに2回表が出る 確率 」を求めるときなどに、 二項分布 の確率関数で利用されています。 このページは、このような人へ向けた内容となっています 組み合わせの計算(\\({}_nC_r\\))が苦手 組み合わせの計算(\\({}_nC_r\\))をよく間違えてしまう 計算量が多くて嫌いなので、もっと簡単に計算できる方法を知りたい 高校数学の組み合わせの単元で登場するコンビネーション(\\({}_nC_r組み合わせと計算 14 minsancom Title みんなの算数オンライン 中学受験4年Unit29 2 場合の数3 組み合わせと計算 Author みんなの算数オンライン Keywords 組み合わせ,コンビネーション,トーナメント,リーグ




苦手を得意に プロが教える算数の勉強法 栄光ゼミナールの中学受験




世界一分かりやすい算数 小6 場合を順序よく整理して
Hello School 算数 場合の数 練習問題 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。前回 https//wwwyoutubecom/watch?v=tpOLtMx_Bfk 次回 https//wwwyoutubecom/watch?v=pq3pJVNZrIU&index=15&list=PLKRhhk0lEyzPV58dAXzmfZle_wg03CLhlC 組合せ 選ぶことが目的(並べる順番は考えない) 東京および近県で中学受験を目指すお子様への算数家庭教師はお任せください。 下記リンク「中学受験算数家庭教師について」をお読みになり、 ページ内の連絡フォームよりご連絡ください。




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長




高校数学 組み合わせ コンビネーション Ncr の計算方法のコツ できるだけ楽に計算しよう 数学の面白いこと 役に立つことをまとめたサイト
そのためには、算数を日常生活に生かすよう様々な場面を捉え、子供に働きかけることが大切です。 なお、ここでの学習は、中学二年生の確率の学習につながります。 6年算数 場合の数(1) イラスト」/横井智美 『小六教育技術』18年12月号より 順列「p」と組み合わせ「c」の使い分け|確率 iPadProを授業で活用していくので、明日からともよし塾が進化します モル計算、濃度計算などの問題解説 レベル組合せ → 印刷用pdf版は別頁 《解説》 並べ方を区別するのが「順列」で,並べ方を区別しないのが「組合せ」です 異なる5個のくだものから,異なる3個のくだものを選ぶ(選ぶだけで並べない)組合せは,次のように,順列から逆算すると分かります



中学受験算数 場合の数




5分で分かる 確率統計 Ncr の計算方法 あぱーブログ
数学において、組合せ(くみあわせ、英 combination, choose )とは、相異なる(あるいは区別可能な)いくつかの要素の集まりからいくつかの要素を(重複無く)選び出す方法である 。 あるいは選び出した要素をその"並べる順番の違いを区別せずに"並べたもののことである 。C 3つから2つ選ぶ組み合わせより2つ減ってるんだ。 C 2,3,4,5,って増えていくんだな。 2つの中から2つを選ぶ組み合わせは1通りしかないことに目を向けさせ,組み合わせの数が,2,3,4,5,と増えていくことを理解させる。11 並べ方と組み合わせ方 学 年 組 氏 名 1 5,6,7の3枚の数字カードを使って,3けたの整数を作ります。このときにでき る整数を小さい順にすべて書きましょう。




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




順列と組み合わせの公式とその違い 問題付き 理系ラボ
1 掲載経緯 東京女学館小学校の小野寺美賀先生は09年5月25日付けの朝日新聞の「花まる先生公開授業」 で紹介されました。それをきっかけとして、取材を行い、資料を提供してくださいました。本稿は提供して頂いた小野寺美香先生の資料のうち、場合の数の授業の意図を紹介します。なおA、B、Cを頂点としたとき、頂点から頂点へ引ける線の数が組み合わせの数になります。 3つから2つを選ぶ場合、三角形となり3本です。 つまり 3通り 。組み合わせの確率を計算 「算数・数学」カテゴリーの人気ランキング 関数グラフ作成 GCalcPlus 式を入力するだけで、グラフを作成する数式グラフ化ソフト 二次元に加え、新しく三次元グラフにも対応 (ユーザー評価: 25);




すきるまドリル 小学6年生 算数 場合の数 無料学習プリント すきるまドリル 無料学習プリント




Newみんなの算数講座14 記念撮影と掃除当番 中学受験の算数知恵宝庫
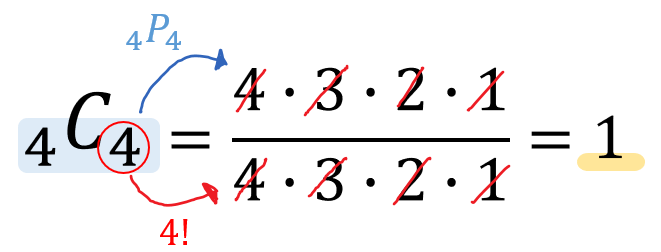
算数への関心・態 度・意欲 順列や組み合わせについて、図や表などを用いて工夫をしながら、 落ちや重なりがないように、順序よく調べようとする。 数学的な考え方 順列や組み合わせについて、落ちや重なりのないように図や表を適第6学年 組 算数科学習指導案 指導者 1単元名場合の数 「順序よく整理して調べよう」 2単元目標 日常的な事象について,起こりうる場合を落ちや重なりがないように工夫して調べようとしてM C n = m × ( m − 1) × ⋯ × ( m − n 1) n × ( n − 1) × ⋯ × 2 × 1 の分母は、 1 から n までのかけ算なので、 n の階乗です。 参考: 階乗の意味と値一覧など つまり、 m C n = m × ( m − 1) × ⋯ × ( m − n 1) n!
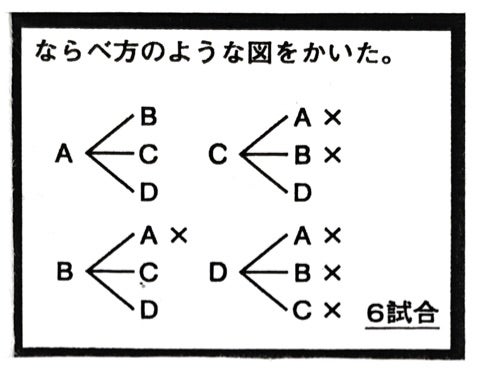



試合の組合せ 算数嫌い0 ゼロ 先生のブログ




Sapix6年生 算数61 16 22 開成への道
組み合わせの計算方法の証明 順列では、「並べる」という操作が入りますが、組み合わせでは「並べる」という操作は除外されます。 例えば、1, 2, 3の三つの数字について、順列の全ての場合を列挙すると次の6通りがあります。 組み合わせでは、上記6つまた,4個のものから3個取る組み合わせの数は, となります。 また, 4 c 3 = 4 c 1 ですから,上の問題では,どのハンカチを残すかを考えても解決することができます。 なお,第6学年の学習としては,表にかいて調べていくとよいでしょう。 場合の数重複組合せ 重複組合せ 《解説》 ※順序が違えば別物として数えるのが「 順列 」,順序だけ違うものは同じものして数えるのが「 組合せ 」 例 異なる2つのものa,bから重複を許して3つとる方法 重複組合せ 重複順列 {a,a,a} {a,a,b}




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




順列と組み合わせ 算数用語集
タテ書き計算器『算ちゃん(M)』 「 × ÷ 」の四則計算をタテ書き組合せ 友達がよくわからないことを言っていたので、調べてみた。 楽しかった。 一日1440分ある時刻から任意で12個抽出すると何通りあるかを調べた。 一日12本しか列車が来ないローカル線の駅の時刻表を見て、ふと思いついた。 桁数がとてつもなく 組み合わせ C とは? 組み合わせとは、 人や物を選び出す/取り出すこと です。 選び出すだけなので、選び出す順番や、選び出したものの並び順は考慮しません。 組み合わせを意味する英単語「Combination」の頭文字をとって記号「\(\mathrm{C}\)」で表します。



組み合わせを書き出す 中学受験算数 場合の数 どう解く 中学受験算数



1
中学受験 4年 unit 292 場合の数3 組み合わせと計算 組み合わせの場合の数の計算! コンビネーションの計算方法 4年生向け 中学受験 算数 場合の数 (組み合わせ計算) 5人から 人を選びます。 コンビネーションを使った計算方法を例題とともに解説 算数における順列・組み合わせの扱いについて 数学(初等組合せ論)における順列について,算数の授業でよく見かけるのは,順列の総数が 4P4 (または4!,4×3×2×1)で表される場面です。 式は「6×4」です。 Google で「算数 学習指導案 順列」を検索し




順列pと組み合わせcの違いと 簡単 な見分け方
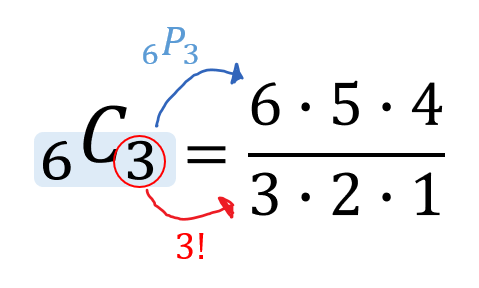



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




順列と組合せの違いと例題 高校数学の美しい物語




順列と組み合わせの公式とその違い 問題付き 理系ラボ




コンビネーション Mcn の計算方法 具体例で学ぶ数学




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
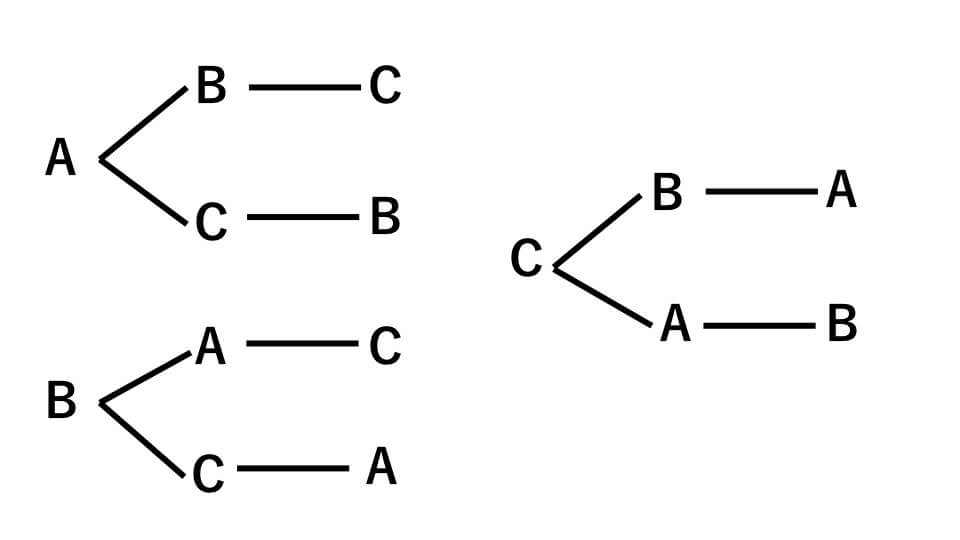



中学受験 算数 場合の数 例題を使ってポイント解説 中学受験アンサー




順列 組合せに頼らない 素朴に数える ための3本柱 わが子を算数 数学嫌いにさせない習慣 朝日新聞edua



1
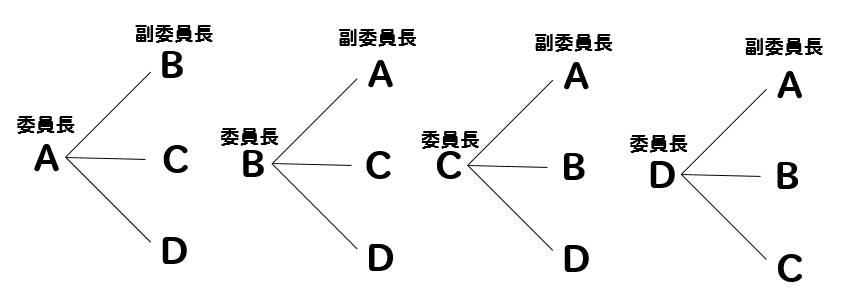



トップ 100 並べ方 と 組み合わせ 方 問題
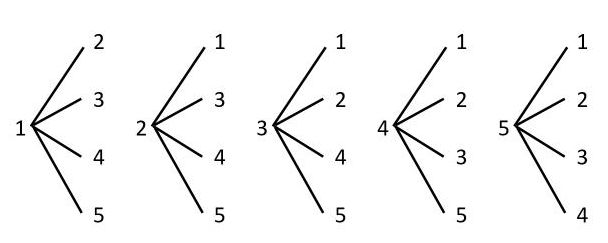



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ
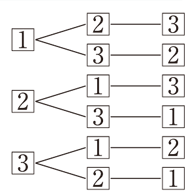



順列と組み合わせ 算数用語集



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S6 0 Pdf
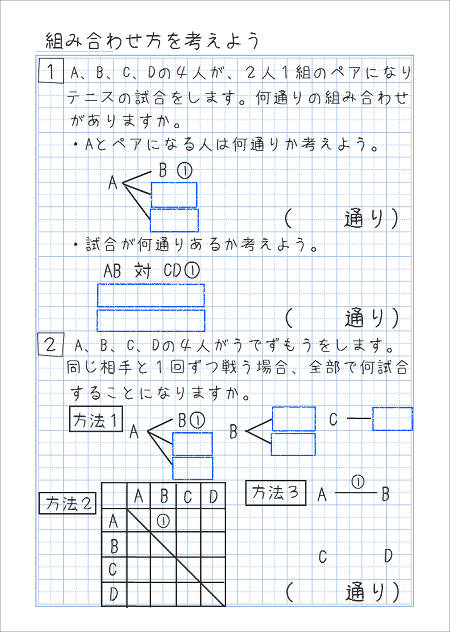



並べ方と組み合わせ方 その1 家庭学習レシピ



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




5講 組合わせ 1章 場合の数と確率 問題集 高校数学a




順列と組合せの違いとその公式とは 応用問題5選もあわせて解説 遊ぶ数学




算数テク 場合の数 プレゼント交換2 中学受験算数なら開成卒プロ家庭教師k



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



小6算数です答え10通りです 組み合わせを教えて下さい 10 Yahoo 知恵袋




トップ 100 並べ方 と 組み合わせ 方 問題




中学2年数学 確率 場合の数を求める問題の解き方 数学の面白いこと 役に立つことをまとめたサイト




組み合わせ C とは 公式や計算方法 は何通り 受験辞典



算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素



樹形図の書き方のコツと注意点 中学受験で 場合の数 をマスターする 中学受験ナビ




難関中学に合格する 算数脳を鍛える図形トレーニング Yell Books Amazon De Bucher




場合の数の公式は暗記してはいけない オンライン授業専門塾ファイ




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



ドリルズ 小学6年生 算数 の無料学習プリント場合の数の問題




小学6年生の算数 動画 組み合わせ方の問題 19ch




中学受験 算数 場合の数 例題を使ってポイント解説 中学受験アンサー



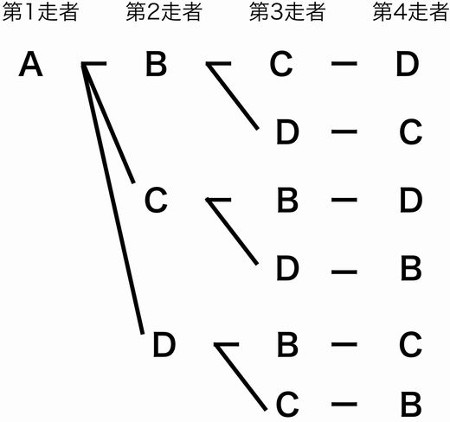
算数の問題です A B C Dの4チームで野球をします どのチーム Yahoo 知恵袋




友tom V Twitter 何が順列pで組み合わせcや なんぼ解説読んでいくら問題読んでも全く使い分け方がわからんわ っていうのを高校とspiの勉強の際に経験し 10年たった今でも全く理解できず解けない模様 小中までの算数と数学は大好きだけど高校数学は大嫌いって




小学6年生の算数 動画 並べ方 組み合わせ方 の問題 19ch




小6 算数 小6 39 組み合わせ方 Youtube
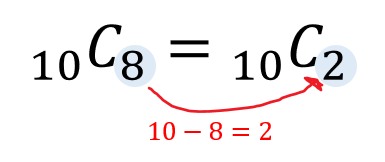



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




第3回 問題 算数オリンピック大会



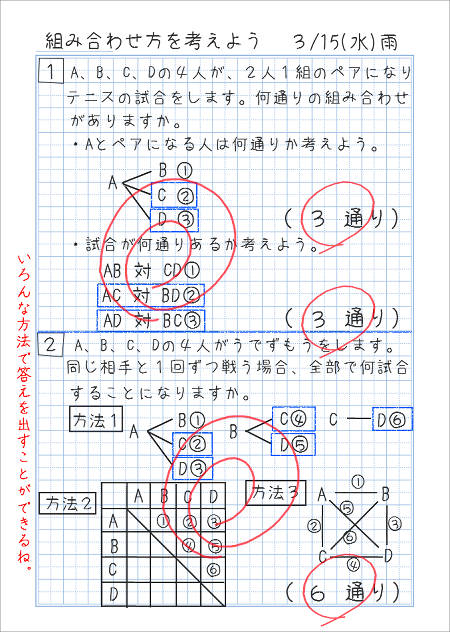
記事 詳細情報 18年 12月 11日 火曜日 6年生 算数 並べ方と組み合わせ方 a b c dの4チームでバスケットボールの試合をします どのチームも 違ったチームと1回ずつ試合をするとき どんな対戦があるか調べましょう この問題
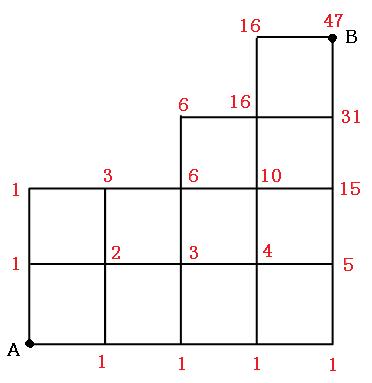



道順を求める場合の数の裏技 場合の数の道順は数字を書きこんでいけ




8月1日 小6算数 夏期講習 期 ジャングルジムブログ




算数における順列 組み合わせの扱いについて かけ算の順序の昔話




小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




すきるまドリル 小学6年生 算数 場合の数 無料学習プリント すきるまドリル 無料学習プリント
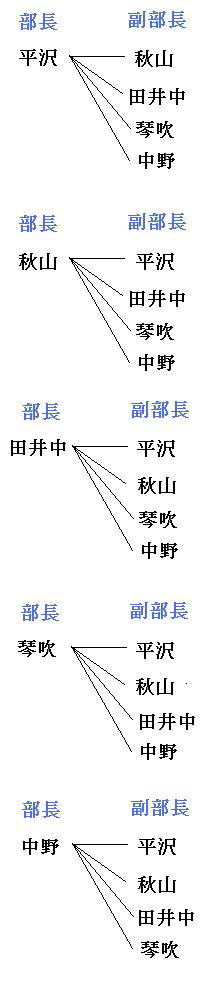



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける
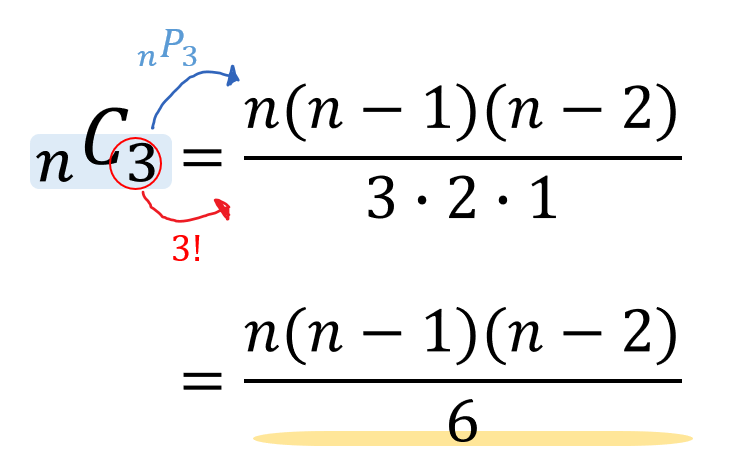



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ
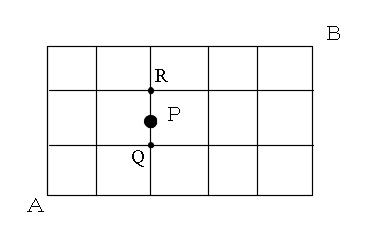



組み合わせの考え方と公式 組み分けと道順を求める問題の解き方




小6 算数 小6 40 並べ方 組み合わせ方 Youtube




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



並べ方と組み合わせ方 その1 家庭学習レシピ




リーグ戦とトーナメント戦 小学校6年教材より 身勝手な主張




場合の数 並べる と 選ぶ の計算方法の違い




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
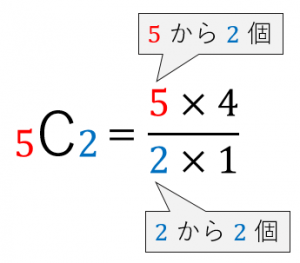



コンビネーション Mcn の計算方法 具体例で学ぶ数学



1



1




スマホok 6年 並べ方と組み合わせ方 場合の数 並べ方を考えよう Youtube




中学受験算数 場合の数 の授業映像 プリント無料配布 Youtube スタディカフェ
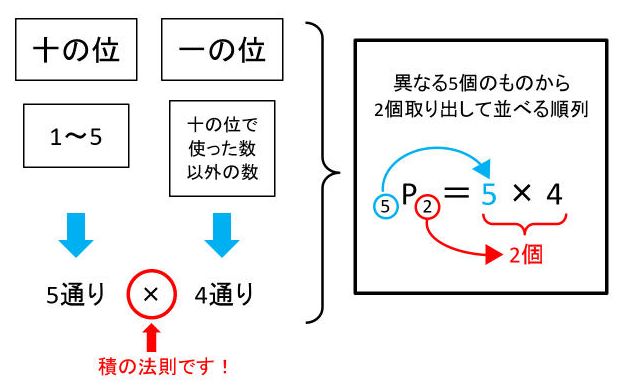



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ



小学生6年生の算数の問題について教えてください の10 15 Yahoo 知恵袋




苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




場合の数 並べる と 選ぶ の計算方法の違い




自宅学習 小6算数 組み合わせ方1 例1 Youtube




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




初等算数 の やってみてね みたいな問題です 答えは来週になるんですけど 組合せとか Clear




並べ方と組み合わせ方 その1 家庭学習レシピ




何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




友tom V Twitter 何が順列pで組み合わせcや なんぼ解説読んでいくら問題読んでも全く使い分け方がわからんわ っていうのを高校とspiの勉強の際に経験し 10年たった今でも全く理解できず解けない模様 小中までの算数と数学は大好きだけど高校数学は大嫌いって




小学6年生の算数 場合の数 順列 練習問題プリント ちびむすドリル 小学生
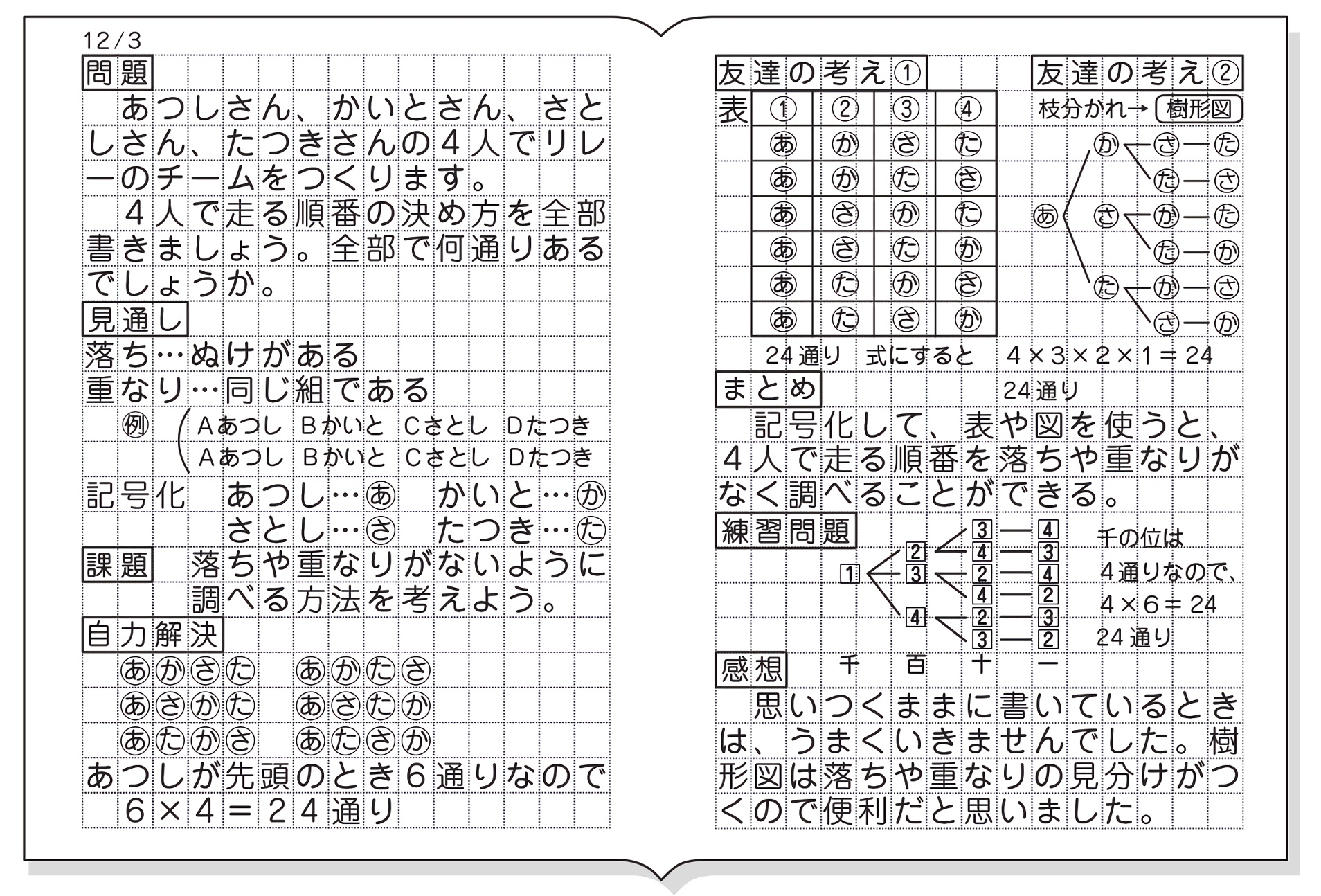



小6算数 場合の数 1 指導アイデア みんなの教育技術




小6算数 場合の数 2 指導アイデア みんなの教育技術




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長



みんなの算数オンライン 教科書レベル 6年 場合の数入門 組み合わせ 例題と解説




組み合わせの公式 高校数学 身勝手な主張




重複組合せはなぜ仕切りを使うの 整数解の個数を求める問題で鍛えよう 遊ぶ数学




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
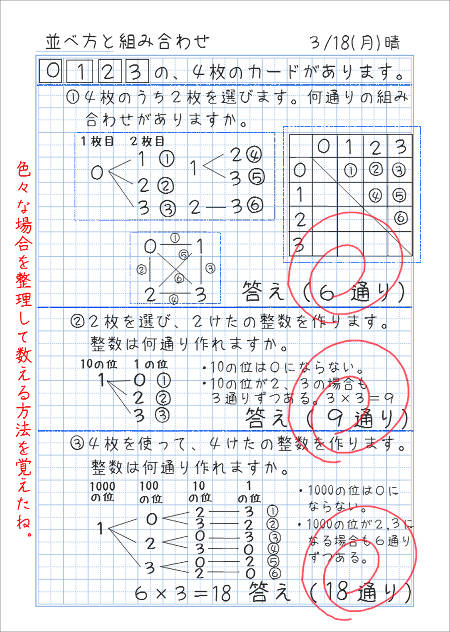



並べ方と組み合わせ方 その2 家庭学習レシピ



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素




算数 場合の数の解き方は 問題別に考え方を解説 数スタ




6年算数場合の数 1 教え方のポイント
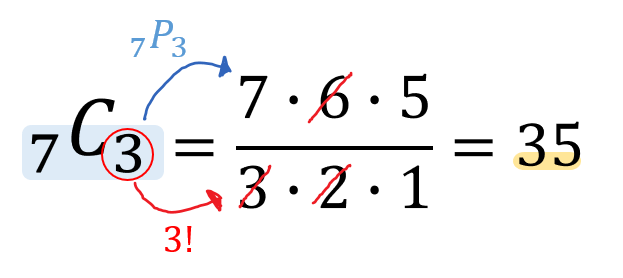



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ




小学校6年生 算数 組み合わせ 順番は関係ないのよ Youtube




高校数学 数a 14 組み合わせ 基本編 Youtube



0 件のコメント:
コメントを投稿